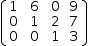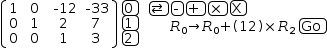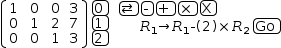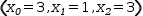5.5 Reduced Row-echelon form
The preceding section shows how to reduce a matrix to row-echelon
form.
However, upon conversion back to linear-equation form,
back substitution
is still required to achieve a solution.
It turns out that back
substitution can be eliminated if more
work is performed on the
matrix. By further reducing the matrix
so there is a 1 on the
diagonals, and zeroes elsewhere (except
for the last column),
conversion to a linear system produces
equations with just a
variable on one side and a constant on the
other –
in other
words, the final solution.
Definition 5.5
A matrix is in reduced row-echelon form if
- it is in row echelon form
- every pivot element is 1 and is the only non-zero element in its
column
Let's see how the Gauss helper can be used to do this.
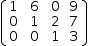 [(1, 6, 0, 9), (0, 1, 2, 7), (0, 0, 1, 3)]
[(1, 6, 0, 9), (0, 1, 2, 7), (0, 0, 1, 3)]
is in row-echelon form but not in reduced row-echelon form.
The first step is to change the 6 in row 0 to a
zero. To to this, subtract 6
times
the second row from the first.
 gaussɱ([(1, 6, 0, 9), (0, 1, 2, 7), (0, 0, 1, 3)], (, "-", 0, 1, 6))
gaussɱ([(1, 6, 0, 9), (0, 1, 2, 7), (0, 0, 1, 3)], (, "-", 0, 1, 6))
The third column of row 0 is now -12,
so we want to add 12 times the
third row onto the first
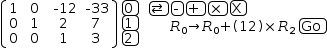 gaussɱ([(1, 0, -12, -33), (0, 1, 2, 7), (0, 0, 1, 3)], (, "+", 0, 2, 12))
gaussɱ([(1, 0, -12, -33), (0, 1, 2, 7), (0, 0, 1, 3)], (, "+", 0, 2, 12))
The second row starts with 0,1 so only the third column needs to be
dealt with. To set it to zero, subtract twice the third row from the
second.
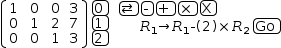 gaussɱ([(1, 0, 0, 3), (0, 1, 2, 7), (0, 0, 1, 3)], (, "-", 1, 2, 2))
gaussɱ([(1, 0, 0, 3), (0, 1, 2, 7), (0, 0, 1, 3)], (, "-", 1, 2, 2))
The final value of the matrix is
 [(1, 0, 0, 3), (0, 1, 0, 1), (0, 0, 1, 3)]
[(1, 0, 0, 3), (0, 1, 0, 1), (0, 0, 1, 3)].
Conversion to linear-equation form gives a direct result:
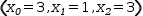 (x_0=3, x_1=1, x_2=3)
(x_0=3, x_1=1, x_2=3).